PLANTEAMIENTO
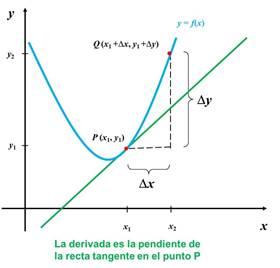
Se ilustra
geométricamente el concepto de derivada de una función.
DERIVADA
DE UNA FUNCIÓN
Se define como derivada de
una función ![]() con respecto a
con respecto a ![]() en un punto
en un punto ![]() ,
al límite, si existe, del cociente de incrementos
,
al límite, si existe, del cociente de incrementos ![]() cuando
cuando
![]() tiende a cero.
tiende a cero.
Esto significa que la
derivada es el límite del cociente del incremento de la variable dependiente,
entre el incremento de la variable independiente, cuando éste tiende a cero, y
se denota por:
![]()
INTERPRETACIÓN
GEOMÉTRICA DE LA DERIVADA
La interpretación geométrica de la derivada es la pendiente de la
recta tangente en el punto ![]() .
.
A medida que la
función crece lo hace también la pendiente de su tangente. Eso significa que la
derivada representa la razón de cambio
de una variable respecto a otra.
El uso de la derivada de una función puede ayudar a determinar si una
función es creciente, decreciente o constante en un intervalo dado:
- Si la derivada es positiva, la función es creciente.
- Si la derivada es negativa, la función es decreciente.
- Si la derivada es cero, la función tiene un punto
crítico (PC) y puede ser un máximo o un mínimo.
CONCLUSIÓN
Conforme
un punto Q de la
curva está mas próximo a P,
la pendiente de la secante que pasa por P
y Q será
un valor más cercano a la pendiente de la recta tangente de la curva en P.
La
derivada de una función ![]() para un argumento x,
es numéricamente igual a la pendiente de la recta tangente a la curva dada por
la función en el punto
para un argumento x,
es numéricamente igual a la pendiente de la recta tangente a la curva dada por
la función en el punto ![]() .
.
PROPUESTA
DE TRABAJO
1.
Mover el punto rojo A de la función y ver el comportamiento
de la pendiente m.
2.
Comprobar que la recta roja es la tangente de la función.
3.
Verificar que a medida que crece más la función, lo hace
también la pendiente m de la tangente.
4.
Acercar el punto A hasta que la pendiente sea muy pequeña.
5.
Encontrar los puntos de la curva con tangente horizontal (es decir
de pendiente cero).
6.
Los puntos ![]() ,
, ![]() y
y ![]() con
tangentes horizontales son los puntos críticos de la función, es decir, son
aquellos cuya derivada es cero y representan los máximos o mínimos de la
función.
con
tangentes horizontales son los puntos críticos de la función, es decir, son
aquellos cuya derivada es cero y representan los máximos o mínimos de la
función.
7.
Pulsar el icono que se sitúa arriba a la derecha para
regresar a la construcción inicial.
8.
Modificar los valores de los
deslizadores para redefinir la función y repetir el proceso.