Page 38 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

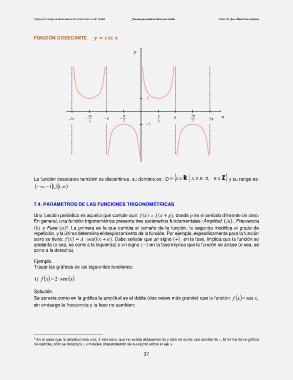
FUNCIÓN COSECANTE =

La función cosecante también es discontinua, su dominio es: D   x R x  n   , n   Z y su rango es:
   , 1   ,1 

7.4. PARÁMETROS DE LAS FUNCIONES TRIGONOMÉTRICAS

Una función periódica es aquella que cumple que: () = ( + ), donde es el periodo diferente de cero.
En general, una función trigonométrica presenta tres parámetros fundamentales: Amplitud   , Frecuencia
A
() y Fase () . La primera es la que cambia el tamaño de la función, la segunda modifica el grado de
4
repetición, y la última determina el desplazamiento de la función. Por ejemplo, específicamente para la función
seno se tiene: () = ∙ sen( + ). Cabe señalar que un signo (+) en la fase, implica que la función se
adelante (o sea, se corre a la izquierda) y un signo (−) en la fase implica que la función se atrase (o sea, se
corre a la derecha).

Ejemplo.
Trazar las gráficas de las siguientes funciones:

1)   xf  2 sen   x

Solución.
Se aprecia como en la gráfica la amplitud es el doble (dos veces más grande) que la función   sen xxf  ,
sin embargo la frecuencia y la fase no cambian:

4 En el caso que la amplitud sea uno, sea cero, que no exista defasamiento y sólo se sume una constante , la forma de la gráfica
no cambia, sólo se desplaza unidades (dependiendo de su signo) sobre el eje .

37