Page 21 - m5-unidad05-polares

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Coordenadas polares Autor: Dr. José Manuel Becerra Espinosa

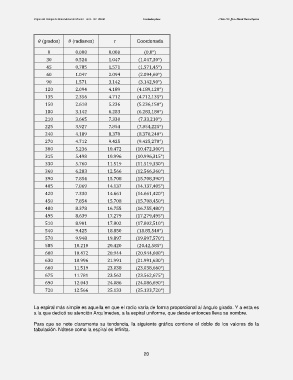
(grados) (radianes) r Coordenada

0 0.000 0.000 (0,0°)
30 0.524 1.047 (1.047,30°)
45 0.785 1.571 (1.571,45°)
60 1.047 2.094 (2.094,60°)
90 1.571 3.142 (3.142,90°)
120 2.094 4.189 (4.189,120°)
135 2.356 4.712 (4.712,135°)
150 2.618 5.236 (5.236,150°)
180 3.142 6.283 (6.283,180°)
210 3.665 7.330 (7.33,210°)
225 3.927 7.854 (7.854,225°)
240 4.189 8.378 (8.378,240°)
270 4.712 9.425 (9.425,270°)
300 5.236 10.472 (10.472,300°)
315 5.498 10.996 (10.996,315°)
330 5.760 11.519 (11.519,330°)
360 6.283 12.566 (12.566,360°)
390 7.854 15.708 (15.708,390°)
405 7.069 14.137 (14.137,405°)
420 7.330 14.661 (14.661,420°)
450 7.854 15.708 (15.708,450°)
480 8.378 16.755 (16.755,480°)
495 8.639 17.279 (17.279,495°)
510 8.901 17.802 (17.802,510°)
540 9.425 18.850 (18.85,540°)
570 9.948 19.897 (19.897,570°)
585 10.210 20.420 (20.42,585°)
600 10.472 20.944 (20.944,600°)
630 10.996 21.991 (21.991,630°)
660 11.519 23.038 (23.038,660°)
675 11.781 23.562 (23.562,675°)
690 12.043 24.086 (24.086,690°)
720 12.566 25.133 (25.133,720°)

La espiral más simple es aquella en que el radio varía de forma proporcional al ángulo girado. Y a esta es
a la que dedicó su atención Arquímedes, a la espiral uniforme, que desde entonces lleva su nombre.

Para que se note claramente su tendencia, la siguiente gráfica contiene el doble de los valores de la
tabulación. Nótese como la espiral es infinita.

20