Page 14 - m5-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Álgebra para analizar los objetos geométricos Autor: Dr. José Manuel Becerra Espinosa

5
y   x  13
2 5
multiplicando por 10 :
10 y  25 x 26  25 x 10 y 26 0

DOS PUNTOS (CARTESIANA)

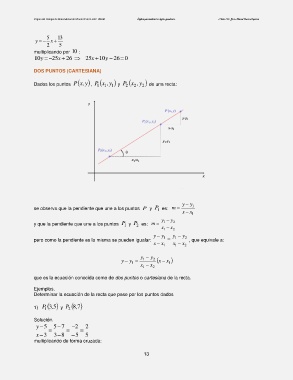
Dados los puntos  y,xP  ,  ,xP 1 1 y 1  y  ,xP 2 2 y 2  de una recta:

y  y
se observa que la pendiente que une a los puntos P y P es: m  x  x 1
1
y  y 1
1
y que la pendiente que une a los puntos P y P es: m  x  x 2 2
2
1
1
y  y y  y
pero como la pendiente es la misma se pueden igualar: 1  1 2 , que equivale a:
x  x 1 x  x 2
1

y  y
1
y  y  x  x 2 x  x 1 
1
1 2
que es la ecuación conocida como de dos puntos o cartesiana de la recta.

Ejemplos.
Determinar la ecuación de la recta que pase por los puntos dados

1)   53,P 1 y   78,P 2

Solución.
y  5  5 7   2  2
x  3 3 8  5 5
multiplicando de forma cruzada:

13