Page 13 - m5-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Álgebra para analizar los objetos geométricos Autor: Dr. José Manuel Becerra Espinosa

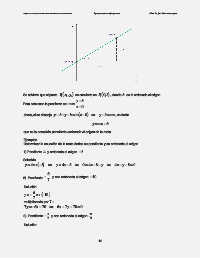
Se advierte que el punto ( ,xP 1 1 y 1 ) se convierte en ( ) b,P 0 , donde b es la ordenada al origen.
1
y −b
Para este caso la pendiente es: m =
x − 0

ahora, si se despeja y − b : y − b = m (x −0 )  y − b = mx , es decir:

y = mx+ b

que es la ecuación pendiente-ordenada al origen de la recta.

Ejemplos.
Determinar la ecuación de la recta dadas su pendiente y su ordenada al origen.

1) Pendiente 4 y ordenada al origen 8−

Solución.
y = 4 +x ( ) 8−  y = 4 −x 8  0 = 4 −x 8− y  4 − yx − 8 = 0

6
2) Pendiente − y con ordenada al origen 10−
7

Solución.
6
y = − x + ( 10− )
7
multiplicando por 7 :
7 =y − 6 −x 70  6 +x 7 +y 70= 0

5 13
3) Pendiente − y con ordenada al origen
2 5

Solución.

12