Page 45 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

8. FUNCIÓN EXPONENCIAL

Una función exponencial con base se define como:

y  f   ax  x

donde a R con a 0 , a  1 y x es un número real.

Esto significa que la base de la función exponencial siempre es positiva, por lo que el valor de   xf siempre
es positivo. Además, la base no puede ser la unidad, porque se convertiría en la función constante
f   1 x x 1.

Es importante que esta función no se confunda con la función   xxf  a , cuya base es que asocia a cada
a
número real un número positivo x . El comportamiento de estas funciones es muy distinto. Para ejemplificar
esto, se toma el valor de a 3 y tabulando ambas funciones, se tiene:

-3 -2 -1 0 1 2 3 4 5 6
f   xx  3 -27 -8 -1 0 1 8 27 64 125 216

x
f   x  3 0.037 0.111 0.333 1 3 9 27 81 243 729

Como puede apreciarse, la diferencia de valores es considerable, ya que en la primera función sólo se
calcula el cubo del número y en la segunda se comporta de forma exponencial.

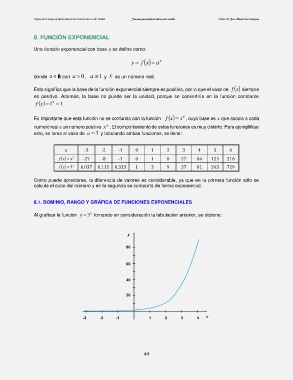
8.1. DOMINIO, RANGO Y GRÁFICA DE FUNCIONES EXPONENCIALES

x
Al graficar la función y  3 tomando en consideración la tabulación anterior, se obtiene:

44