Page 3 - m5-unidad10-parabola

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Parábola Autor: Dr. José Manuel Becerra Espinosa

desarrollando:

2
2
2
2
x  2xp  p  y  x  2xp  p
2

eliminando términos queda:
2
 2 xp y  2 xp

o bien:

2
y  2 xp 2 xp

que es igual a:

2
y  4 px

ecuación conocida como ecuación ordinaria o canónica de la parábola con vértice en el origen.

EP
A la recta que pasa por el vértice y el foco se le conoce como eje de la parábola  .

Cabe señalar que en una parábola la excentricidad siempre es uno porque la distancia que hay del vértice
al foco es igual a la que hay del vértice a la directriz.

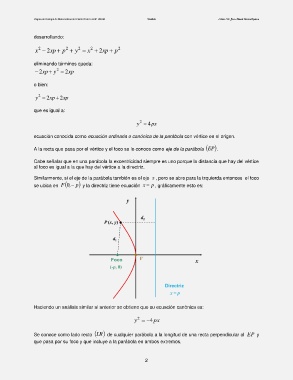
Similarmente, si el eje de la parábola también es el eje x , pero se abre para la izquierda entonces el foco
se ubica en  ,F 0   p y la directriz tiene ecuación x  p , gráficamente esto es:

Haciendo un análisis similar al anterior se obtiene que su ecuación canónica es:

2
y   4 px

LR
Se conoce como lado recto   de cualquier parábola a la longitud de una recta perpendicular al EP y
que pasa por su foco y que incluye a la parábola en ambos extremos.

2