Page 7 - m5-unidad10-parabola
P. 7
Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Parábola Autor: Dr. José Manuel Becerra Espinosa
pero de la figura se aprecia que: x ' x h y y ' y k
o sea : x ' x h y y ' y k
por lo tanto si se sustituye en la ecuación con los ejes trasladados se tiene:
y k 2 4 p x h
que es la ecuación trasladada de la parábola con vértice en k,h con EP : eje x
El vértice en este caso está en: k,hV
El foco se ubica en: hF k , p
La ecuación de la directriz es: x h p
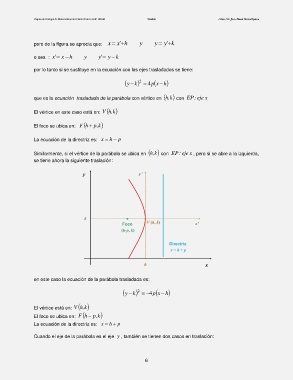
Similarmente, si el vértice de la parábola se ubica en k,h con EP : eje x , pero si se abre a la izquierda,
se tiene ahora la siguiente traslación:
en este caso la ecuación de la parábola trasladada es:
y k 2 4 p x h
El vértice está en: k,hV
El foco se ubica en: hF k , p
La ecuación de la directriz es: x h p
Cuando el eje de la parábola es el eje y , también se tienen dos casos en traslación:
6