Page 6 - m5-unidad10-parabola

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Parábola Autor: Dr. José Manuel Becerra Espinosa

2
4) x = − 7 y

Solución.
7
4 =p − 7  p = − . EP : eje y . Signo (-), por lo que se abre hacia abajo. El foco se ubica en
4
 7  7  7 
F  −0,  . La ecuación de la directriz es: y = . El lado recto es: LR = 4  = 7 . u
 4  4  4 

5) Hallar la ecuación de la parábola cuyo foco se ubica en ( ) 03,F y vértice en el origen.

Solución.
2
2
EP : eje x . =p 3  y = x ) 3 ( 4  y = 12 x . La ecuación de la directriz es: =x − 3 . Como el signo
es (+) se abre hacia la derecha. El lado recto es: LR = ) 3 ( 4 = 12 . u

6) Hallar la ecuación de la parábola cuya ecuación de su directriz es =y 9 y vértice en el origen.

Solución.
2
2
EP : eje y . p = 9  x = − 4 ( )y9  x = − 36 y . El foco se ubica en ( ) 90,F . Como el signo es (-)
se abre hacia abajo. El lado recto es: LR = ( 4 − ) 9 = 36 . u

2. TRASLACIÓN DE EJES COORDENADOS

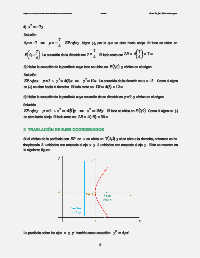
Si el vértice de la parábola con EP en x se ubica en ( ) k,hV y si se abre a la derecha, entonces se ha

desplazado h unidades con respecto al eje x y k unidades con respecto al eje y . Esto se muestra en
la siguiente figura:

2
La parábola sobre los ejes 'x y 'y tendría como ecuación: 'y = 4px '

5