Page 3 - m5-unidad15-regresion

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Regresión lineal simple Autor: Dr. José Manuel Becerra Espinosa

Una relación positiva entre y significa que los valores crecientes de están asociados con los valores
crecientes de . Una relación negativa significa que los valores crecientes de están asociados con los
valores decrecientes de .

La distribución conjunta de dos variables puede expresarse gráficamente mediante un diagrama de
dispersión: en un plano se representa cada elemento observado haciendo que sus coordenadas sobre los
ejes cartesianos sean los valores que toman las dos variables para esa observación.

Un diagrama de dispersión se usa para descubrir y mostrar las relaciones entre dos conjuntos asociados
de datos y confirmar relaciones anticipadas entre dos conjuntos asociados de datos.

Ejemplo.
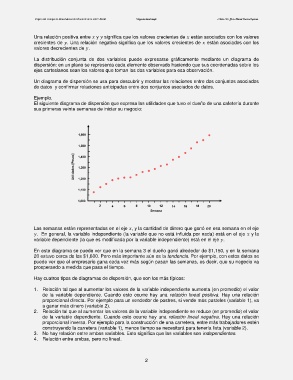
El siguiente diagrama de dispersión que expresa las utilidades que tuvo el dueño de una cafetería durante
sus primeras veinte semanas de iniciar su negocio:

Las semanas están representadas en el eje , y la cantidad de dinero que ganó en esa semana en el eje
. En general, la variable independiente (la variable que no está influida por nada) está en el eje y la
variable dependiente (la que es modificada por la variable independiente) está en el eje .

En este diagrama se puede ver que en la semana 3 el dueño ganó alrededor de $1,150, y en la semana
20 estuvo cerca de los $1,600. Pero más importante aún es la tendencia. Por ejemplo, con estos datos se
puede ver que el empresario gana cada vez más según pasan las semanas, es decir, que su negocio va
prosperando a medida que pasa el tiempo.

Hay cuatros tipos de diagramas de dispersión, que son los más típicos:

1. Relación tal que al aumentar los valores de la variable independiente aumenta (en promedio) el valor
de la variable dependiente. Cuando esto ocurre hay una relación lineal positiva. Hay una relación
proporcional directa. Por ejemplo para un vendedor de postres, si vende más pasteles (variable 1), va
a ganar más dinero (variable 2).
2. Relación tal que al aumentar los valores de la variable independiente se reduce (en promedio) el valor
de la variable dependiente. Cuando esto ocurre hay una relación lineal negativa. Hay una relación
proporcional inversa. Por ejemplo para la construcción de una carretera, entre más trabajadores estén
construyendo la carretera (variable 1), menos tiempo se necesitará para tenerla lista (variable 2).
3. No hay relación entre ambas variables. Esto significa que las variables son independientes.
4. Relación entre ambas, pero no lineal.

2