Page 7 - m5-unidad15-regresion

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Regresión lineal simple Autor: Dr. José Manuel Becerra Espinosa

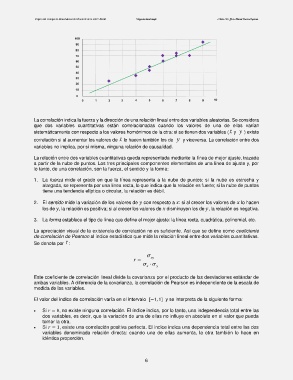
La correlación indica la fuerza y la dirección de una relación lineal entre dos variables aleatorias. Se considera
que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían
sistemáticamente con respecto a los valores homónimos de la otra: si se tienen dos variables (x y y ) existe
correlación si al aumentar los valores de x lo hacen también los de y y viceversa. La correlación entre dos
variables no implica, por sí misma, ninguna relación de causalidad.

La relación entre dos variables cuantitativas queda representada mediante la línea de mejor ajuste, trazada
a partir de la nube de puntos. Los tres principales componentes elementales de una línea de ajuste y, por
lo tanto, de una correlación, son la fuerza, el sentido y la forma:

1. La fuerza mide el grado en que la línea representa a la nube de puntos: si la nube es estrecha y
alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos
tiene una tendencia elíptica o circular, la relación es débil.

2. El sentido mide la variación de los valores de con respecto a : si al crecer los valores de lo hacen
los de , la relación es positiva; si al crecer los valores de disminuyen los de , la relación es negativa.

3. La forma establece el tipo de línea que define el mejor ajuste: la línea recta, cuadrática, polinomial, etc.

La apreciación visual de la existencia de correlación no es suficiente. Así que se define como coeficiente
de correlación de Pearson al índice estadístico que mide la relación lineal entre dos variables cuantitativas.
Se denota por r :


r  xy
 x   y

Este coeficiente de correlación lineal divide la covarianza por el producto de las desviaciones estándar de
ambas variables. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de
medida de las variables.

El valor del índice de correlación varía en el intervalo [−1, 1] y se interpreta de la siguiente forma:

 Si = 0, no existe ninguna correlación. El índice indica, por lo tanto, una independencia total entre las
dos variables, es decir, que la variación de una de ellas no influye en absoluto en el valor que pueda
tomar la otra.
 Si = 1, existe una correlación positiva perfecta. El índice indica una dependencia total entre las dos
variables denominada relación directa: cuando una de ellas aumenta, la otra también lo hace en
idéntica proporción.

6