Page 6 - m5-unidad15-regresion

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Regresión lineal simple Autor: Dr. José Manuel Becerra Espinosa

La correlación es una herramienta poderosa ya que ofrece información valiosa acerca de la relación entre
las variables. Se utiliza para entender dos aspectos:

 Si la relación es positiva o negativa.

 La fuerza de la relación.

En el caso del ingreso familiar y el gasto familiar, es fácil ver que ambos suben o bajan juntos en la misma
dirección. Esto se denomina correlación positiva.

En caso del precio y la demanda, el cambio se produce en la dirección opuesta, de modo que el aumento
de uno está acompañado de un descenso en el otro. Esto se conoce como correlación negativa.

Ejemplo.
Las propinas que obtuvo un mesero en una cocina económica durante diez días están dadas en la siguiente
tabla:

Horas de trabajo 2 4 5 5 6 6 7 7 8 9
Sueldo en pesos 25 35 45 50 60 70 75 70 70 95

Los pares de valores { (2,25), (4,35), (5,45), (5,50), (6,60), (6,70), (7,75), (7,70), (8,70), (9,95) }, forman la
distribución bidimensional en la que hay cierta tendencia a que cuantas más horas de trabajo tiene, sus
ingresos aumentan.

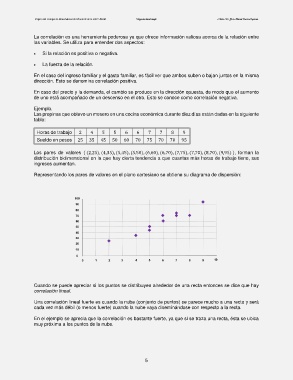
Representando los pares de valores en el plano cartesiano se obtiene su diagrama de dispersión:

Cuando se puede apreciar si los puntos se distribuyen alrededor de una recta entonces se dice que hay
correlación lineal.

Una correlación lineal fuerte es cuando la nube (conjunto de puntos) se parece mucho a una recta y será
cada vez más débil (o menos fuerte) cuando la nube vaya diseminándose con respecto a la recta.

En el ejemplo se aprecia que la correlación es bastante fuerte, ya que si se traza una recta, ésta se ubica
muy próxima a los puntos de la nube.

5