Page 3 - m5-unidad05-polares

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Coordenadas polares Autor: Dr. José Manuel Becerra Espinosa

Generalmente, mientras no se pida expresamente otra cosa, se escoge de las infinitas soluciones,
aquella que corresponde a un valor de positivo y un valor de comprendido en el intervalo
[0, 2]. Al par así escogido se le denomina par principal de coordenadas polares del punto.

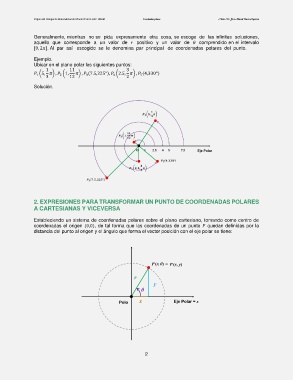
Ejemplo.
Ubicar en el plano polar los siguientes puntos:
1 11 3
(5, ) , (1, 12 ) , (7.5,225°), (2.5, ) , (4,330°)
2
1
5
3
4
3
2

Solución.

2. EXPRESIONES PARA TRANSFORMAR UN PUNTO DE COORDENADAS POLARES
A CARTESIANAS Y VICEVERSA

Estableciendo un sistema de coordenadas polares sobre el plano cartesiano, tomando como centro de
coordenadas el origen (0,0), de tal forma que las coordenadas de un punto quedan definidas por la
distancia del punto al origen y el ángulo que forma el vector posición con el eje polar se tiene:

2