Page 8 - m5-unidad05-polares

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Coordenadas polares Autor: Dr. José Manuel Becerra Espinosa

1 2 3 4 5 6 7

6 6 6 6 6 6 6

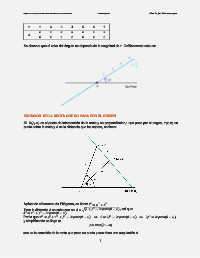
Se observa que el valor del ángulo no depende de la magnitud de . Gráficamente esto es:

ECUACIÓN DE LA RECTA QUE NO PASA POR EL ORIGEN

Si (, ) es el punto de intersección de la recta y su perpendicular  que pasa por el origen, (, ) un
punto sobre la recta y es la distancia que los separa, se tiene:

Aplicando el teorema de Pitágoras, se tiene: = +
2
2
2
2
2
Pero la distancia se sabe que es: = √ + − 2( − ), así que:
= + − 2( − )
2
2
2
2
2
2
Por lo que: = + + − 2( − )  0 = 2 − 2( − )  2 = 2( − )
2
2
2
y simplificando se llega a:
 = ( − )

que es la ecuación de la recta que pasa un punto y que tiene una angulación .
7