Page 22 - m5-unidad06-vectores

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Vectores Autor: Dr. José Manuel Becerra Espinosa

⃗⃗
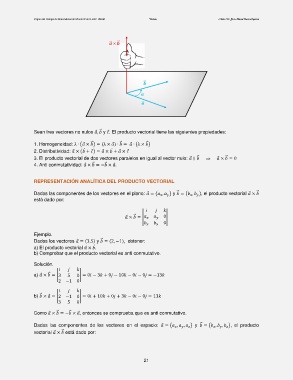
Sean tres vectores no nulos ⃗, y ⃗. El producto vectorial tiene las siguientes propiedades:

⃗⃗
⃗⃗
⃗⃗
1. Homogeneidad: λ ∙ (⃗ × ) = (λ × ⃗) ∙ = ⃗ ∙ (λ × )
⃗⃗
⃗⃗
2. Distributividad: ⃗ × ( + ⃗) = ⃗ × + ⃗ × ⃗
⃗⃗
⃗⃗
3. El producto vectorial de dos vectores paralelos en igual al vector nulo: ⃗ ∥  ⃗ × = 0
⃗⃗
⃗⃗
4. Anti conmutatividad: ⃗ × = − × ⃗.

REPRESENTACIÓN ANALÍTICA DEL PRODUCTO VECTORIAL

⃗⃗
Dadas las componentes de los vectores en el plano: ⃗ = ( , ) y = ( , ), el producto vectorial ⃗ ×
⃗⃗

está dado por:

⃗⃗
⃗ × = | 0 |
0

Ejemplo.
⃗⃗
Dados los vectores ⃗ = (3,5) y = (2, −1), obtener:
⃗⃗
a) El producto vectorial ⃗ × .
b) Comprobar que el producto vectorial es anti conmutativo.

Solución.

⃗⃗
a) ⃗ × = |3 5 0| = 0 − 3 + 0 − 10 − 0 − 0 = −13
2 −1 0

⃗⃗
b) × ⃗ = |2 −1 0| = 0 + 10 + 0 + 3 − 0 − 0 = 13
3 5 0

⃗⃗
⃗⃗
Como ⃗ × = − × ⃗, entonces se comprueba que es anti conmutativo.

⃗⃗
Dadas las componentes de los vectores en el espacio: ⃗ = ( , , ) y = ( , , ), el producto

⃗⃗
vectorial ⃗ × está dado por:

21