Page 19 - m5-unidad06-vectores

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Vectores Autor: Dr. José Manuel Becerra Espinosa

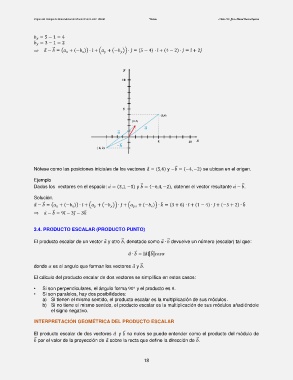
= 5 − 1 = 4

= 3 − 1 = 2

⃗⃗
 ⃗ − = ( + (− )) ∙ ̂ + ( + (− )) ∙ ̂ = (5 − 4) ∙ ̂ + (4 − 2) ∙ ̂ = ̂ + 2̂

⃗⃗
Nótese como las posiciones iniciales de los vectores ⃗ = (5,4) y − = (−4, −2) se ubican en el origen.

Ejemplo
⃗⃗
⃗⃗
Dados los vectores en el espacio: ⃗ = (3,1, −5) y = (−6,4, −2), obtener el vector resultante ⃗ − .

Solución.
⃗⃗
̂
̂
⃗ − = ( + (− )) ∙ ̂ + ( + (− )) ∙ ̂ + ( + (− )) ∙ = (3 + 6) ∙ ̂ + (1 − 4) ∙ ̂ + (−5 + 2) ∙

̂
⃗⃗
 ⃗ − = 9̂ − 3̂ − 3

3.4. PRODUCTO ESCALAR (PRODUCTO PUNTO)

⃗⃗
⃗⃗
El producto escalar de un vector ⃗ y otro , denotado como ⃗ ∙ devuelve un número (escalar) tal que:

⃗⃗
⃗⃗
⃗ ∙ = |⃗|||

⃗⃗
donde es el angulo que forman los vectores ⃗ y .

El cálculo del producto escalar de dos vectores se simplifica en estos casos:

• Si son perpendiculares, el ángulo forma 90° y el producto es 0.
• Si son paralelos, hay dos posibilidades:
a) Si tienen el mismo sentido, el producto escalar es la multiplicación de sus módulos.
b) Si no tiene el mismo sentido, el producto escalar es la multiplicación de sus módulos añadiéndole
el signo negativo.

INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO ESCALAR

⃗⃗
El producto escalar de dos vectores ⃗ y no nulos se puede entender como el producto del módulo de
⃗⃗
⃗⃗
por el valor de la proyección de ⃗ sobre la recta que define la dirección de .
18