Page 15 - m5-unidad15-regresion
P. 15
Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Regresión lineal simple Autor: Dr. José Manuel Becerra Espinosa
Para obtener el número de campeonatos esperados por un atleta en 16 años de competencia, se sustituye
= 16, de manera que sustituyéndolo en la ecuación de la recta, se obtiene:
y . 0 6986 016 . 4303
y 11 . 1776 . 0 4303
y 11 . 6079
Es decir, se pueden esperar aproximadamente entre once y doce campeonatos de un atleta con 16 años
compitiendo.
Para la segunda pregunta, se tiene como dato que = 11, o sea 11 campeonatos, de manera que
sustituyendo en la ecuación de la recta, se obtiene:
11 . 0 6986 x . 0 4303
. 0 6986 x 11 . 0 4303
. 0 6986 x 10 . 5697
10 . 5697
x 15 . 1298
. 0 6986
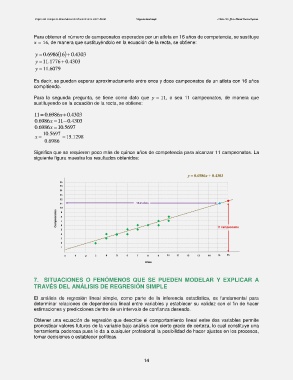
Significa que se requieren poco más de quince años de competencia para alcanzar 11 campeonatos. La
siguiente figura muestra los resultados obtenidos:
7. SITUACIONES O FENÓMENOS QUE SE PUEDEN MODELAR Y EXPLICAR A
TRAVÉS DEL ANÁLISIS DE REGRESIÓN SIMPLE
El análisis de regresión lineal simple, como parte de la inferencia estadística, es fundamental para
determinar relaciones de dependencia lineal entre variables y establecer su validez con el fin de hacer
estimaciones y predicciones dentro de un intervalo de confianza deseado.
Obtener una ecuación de regresión que describe el comportamiento lineal entre dos variables permite
pronosticar valores futuros de la variable bajo análisis con cierto grado de certeza, lo cual constituye una
herramienta poderosa pues le da a cualquier profesional la posibilidad de hacer ajustes en los procesos,
tomar decisiones o establecer políticas.
14