Page 12 - m5-unidad15-regresion

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Regresión lineal simple Autor: Dr. José Manuel Becerra Espinosa

b = y − m x 

Ejemplo.
Obtener y graficar la recta de regresión con los datos las ventas de las pantallas de televisiones del ejemplo
anterior.

Solución.
Los valores obtenidos de la covarianza y de la desviación estándar de la venta de pantallas son:
 xy = − . 2 75
 x = . 1 7078

 − . 2 75
 m = xy = = − . 0 9428
 x 2 ( 7078.1 ) 2
Considerando que x = 5 . 3 y que y = 5 . 6
b = y − m  x = 5 . 6 − ( 0− . 9428 )( ) 95.3 = . 799
Por lo que la recta de regresión lineal es: =y − . 0 9428 +x . 9 799
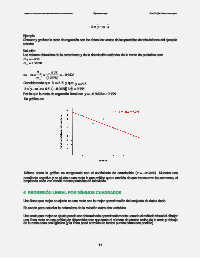
Su gráfica es:

Nótese como la gráfica es congruente con el coeficiente de correlación ( =r − . 0 9428 ) . Muestra una
pendiente negativa y se ajusta a una recta lo que ratifica que a medida de que transcurren las semanas, el
empleado cada vez vende menos pantallas de televisión.

6. REGRESIÓN LINEAL POR MÍNIMOS CUADRADOS

Una línea que mejor se ajusta es una recta con la mejor aproximación del conjunto de datos dado.

Es usada para estudiar la naturaleza de la relación entre dos variables.

Una recta que mejor se ajusta puede ser determinada aproximadamente usando el método visual al dibujar
una línea recta en una gráfica de dispersión para que tanto el número de puntos arriba de la recta y debajo
de la recta sean casi iguales (y la línea pasa a través de tantos puntos como sea posible).

11