Page 11 - m5-unidad15-regresion

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Regresión lineal simple Autor: Dr. José Manuel Becerra Espinosa

5. REGRESIÓN LINEAL POR COVARIANZA

La regresión lineal permite hallar el valor esperado de una variable aleatoria cuando otra variable toma un
valor específico. La aplicación de este método implica un supuesto de linealidad cuando se presenta un
comportamiento creciente o decreciente, por tal razón, se hace indispensable que previo a la selección de
este método exista un análisis de regresión que determine la intensidad de las relaciones entre las variables
que componen el modelo.

El modelo de regresión lineal simple es un modelo óptimo para patrones de tendencia (creciente o
decreciente), es decir, patrones que presenten una relación de linealidad entre las variables.

El objetivo de un análisis de regresión es determinar la relación que existe entre una variable dependiente
y una o más variables independientes. Para poder realizar esta relación, se debe postular una
relación funcional entre las variables.

Cuando se trata de una variable independiente, la forma funcional que más se utiliza en la práctica es la
relación lineal. El análisis de regresión entonces determina la intensidad entre las variables a través de
coeficientes de correlación y determinación.

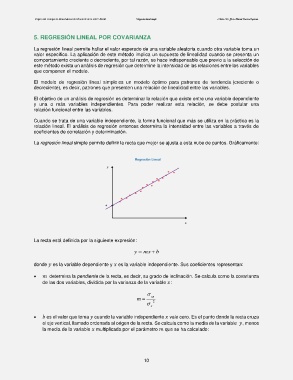
La regresión lineal simple permite definir la recta que mejor se ajusta a esta nube de puntos. Gráficamente:

La recta está definida por la siguiente expresión:

y  mx  b

donde es la variable dependiente y es la variable independiente. Sus coeficientes representan:

 determina la pendiente de la recta, es decir, su grado de inclinación. Se calcula como la covarianza
de las dos variables, dividida por la varianza de la variable :


m  xy
 x 2

 es el valor que toma cuando la variable independiente vale cero. Es el punto donde la recta cruza
el eje vertical, llamado ordenada al origen de la recta. Se calcula como la media de la variable , menos
la media de la variable multiplicada por el parámetro que se ha calculado:

10