Page 30 - m4-unidad05

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Inecuaciones para modelar restricciones Autor: Dr. José Manuel Becerra Espinosa

Para = 0, se tiene:
1 1 1
(0) + = 100  = 100  = 100(2) = 200
3 2 2
Entonces el primer punto es (0,200).
1

Para = 0, se tiene:
1 1 1
+ (0) = 100  = 100  = 300
3 2 3
Entonces el segundo punto es (300,0).
2

Evaluando la segunda ecuación en dos valores distintos:

Para = 0, se tiene:
1 1 1
(0) + = 80  = 80  = 80(6) = 480
3 6 6
Entonces el primer punto es (0,480).
1

Para = 0, se tiene:
1 1 1
+ (0) = 80  = 80  = 240
3 6 3
Entonces el segundo punto es (240,0).
2

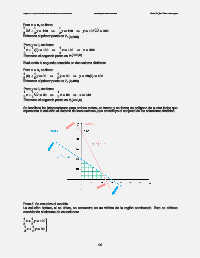
Se localizan las intersecciones para ambas rectas, se trazan y se forma un polígono de cuatro lados que
representa la solución al sistema de inecuaciones, que constituye el conjunto de las soluciones factibles.

Paso 5. Se resuelve el modelo.
La solución óptima, si es única, se encuentra en un vértice de la región sombreada. Esto se obtiene
resolviendo el sistema de ecuaciones:

1 1
+ = 100
3 2 }
1 1
+ = 80
3 6

29