Page 25 - m4-unidad05

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Inecuaciones para modelar restricciones Autor: Dr. José Manuel Becerra Espinosa

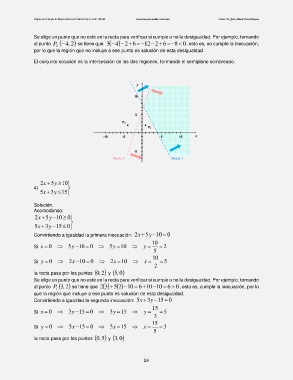
Se elige un punto que no esté en la recta para verificar si cumple o no la desigualdad. Por ejemplo, tomando
al punto  4,P   2 se tiene que   243    6  12 2 6  8 0, esto es, no cumple la inecuación,
2
por lo que la región que no incluye a ese punto es solución de esta desigualdad.

El conjunto solución es la intersección de las dos regiones, formando el semiplano sombreado.

2x 5y 10 
4) 
5x 3y 15 

Solución.
Acomodando:
2x 5y 10   0
5x 3y 15  0 

Convirtiendo a igualdad la primera inecuación: 2 x 5 y 10  0
10
Si x 0  5 y 10  0  5 y 10  y   2
5
10
Si y 0  2 x 10  0  2 x 10  x   5
2
la recta pasa por los puntos   20, y  05, 
Se elige un punto que no esté en la recta para verificar si cumple o no la desigualdad. Por ejemplo, tomando
al punto  23,P 1  se tiene que     102532    6 10 10  6  0, esto es, cumple la inecuación, por lo
que la región que incluye a ese punto es solución de esta desigualdad.
Convirtiendo a igualdad la segunda inecuación: 5 x 3 y 15  0
15
Si x 0  3 y 15  0  3 y 15  y   5
3
15
Si y 0  5 x 15  0  5 x 15  x   3
5
la recta pasa por los puntos  50,  y   03,

24