Page 21 - m5-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Álgebra para analizar los objetos geométricos Autor: Dr. José Manuel Becerra Espinosa

C  20 5
b   1    
Ahora: Para L1: 1
B 1  16 4
C  10 5
b   1    
Para L2: 2
B 1  8 4
como b  b , las rectas además son coincidentes.
2
1

Nótese que si alguna de las ecuaciones se puede expresar como un producto de un número por la otra
entonces las rectas son coincidentes. En este ejemplo si la recta L2 se multiplica por dos se obtiene L1.

3) Obtener la ecuación de la recta que pase por el punto  4,P   6 y que sea paralela a la recta
16 x 3 y 18 0

Solución.
A 16 16
Al ser paralelas m  m , entonces: m   B 1    3  3  m 2
1
1
2
1
aplicando la ecuación punto pendiente de la recta:
16
y  6   x  4   3 y 6  16  x  4  3 y 18  16 x 64
3
 0  16 x 64 3 y 18  16 x 3 y 82 0

PERPENDICULARIDAD

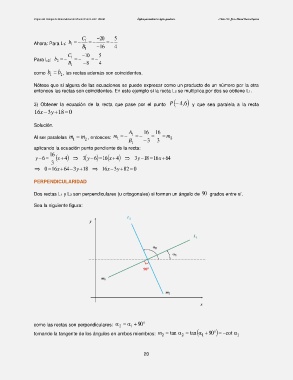
Dos rectas L1 y L2 son perpendiculares (u ortogonales) si forman un ángulo de 90 grados entre sí.

Sea la siguiente figura:

como las rectas son perpendiculares:  2   1 90 

tomando la tangente de los ángulos en ambos miembros: m 2  tan  2  tan  1  90   cot  1

20