Page 4 - m5-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Álgebra para analizar los objetos geométricos Autor: Dr. José Manuel Becerra Espinosa

1.2. DISTANCIA ENTRE DOS PUNTOS

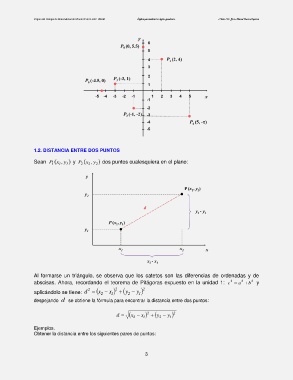
Sean P 1 x 1 , y 1  y P 2 x 2 y , 2  dos puntos cualesquiera en el plano:

Al formarse un triángulo, se observa que los catetos son las diferencias de ordenadas y de
2
2
2
abscisas. Ahora, recordando el teorema de Pitágoras expuesto en la unidad 1: c  a  b y
2
2
2
aplicándolo se tiene: d  x  x 1  y  2 y 1 
2
despejando d se obtiene la fórmula para encontrar la distancia entre dos puntos:

2
2
d  x  x 1   y  y 1 
2
2

Ejemplos.
Obtener la distancia entre los siguientes pares de puntos:

3