Page 6 - m5-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Álgebra para analizar los objetos geométricos Autor: Dr. José Manuel Becerra Espinosa

P  d  d  d  34  52  50  5 .83  7 .21 7 .07  20 .11 . u
3
1
2

Ejemplo.
Sea el punto 4 ,P  3 y el punto  10,xP , obtener la abscisa de P de tal manera que la distancia que los
1 2 2
separe sea 15 unidades.

Solución.
Sustituyendo los datos en la fórmula se tiene:
2
15   x  4 2   10     3 2  x  4 2  13   x  4 2  169
despejando x se tendrán dos soluciones de x :
2
2
2
2
15   x  4  169  225  169   x  4  56  x  4  56
x 1  11 . 48 y x 2  . 3  48 , por lo que los puntos buscados son aproximadamente:
P 1  48.11 , 10  y el punto  .3P 1 48 , 10 

1.3. DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA

Dividir un segmento dirigido en una razón dada significa segmentarlo en partes de forma tal que se
encuentren las coordenadas de un punto  ,xP  y que satisface la comparación entre dos magnitudes. En
a
general, si la razón es de la forma r , implica que el segmento se divide en a  b partes. Por ejemplo,
b
7
si r , el segmento se divide en 11 partes iguales.
4

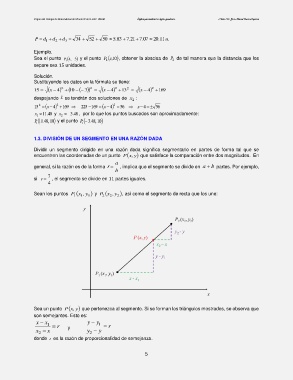
Sean los puntos P 1 x 1 , y 1  y P 2 x 2 y , 2 , así como el segmento de recta que los une:

Sea un punto  ,xP  y que pertenezca al segmento. Si se forman los triángulos mostrados, se observa que
son semejantes. Esto es:
x  x 1  y  y 1  r
x  x r y y  y
2
2
donde r es la razón de proporcionalidad de semejanza.

5