Page 19 - m5-unidad04
P. 19
Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Estadística para interpretar grandes cantidades de datos Autor: Dr. José Manuel Becerra Espinosa
Ahora, se calculan la:
La frecuencia ( ) que es el número de datos que pertenece a cada intervalo de clase.
La frecuencia relativa ( ), que es la frecuencia de cada una de las clases dividida entre el número total
de datos ()
La frecuencia acumulada ( ) que son los datos acumulados desde el primer dato hasta la i-ésima clase.
La frecuencia acumulada relativa ( ) que es la frecuencia acumulada de la clase i-ésima entre el número
total de datos ().
Por lo que la tabla completa queda de la siguiente forma:
Intervalos de clase Marcas Frecuencia Frecuencia Frecuencia
Límite Límite Frecuencia Acumulada
Clase de clase Relativa acumulada
Inferior Superior relativa
1 49.10 49.61 49.36 5 0.06 5 0.06
2 49.61 50.12 49.87 6 0.08 11 0.14
3 50.12 50.63 50.38 12 0.15 23 0.29
4 50.63 51.14 50.89 18 0.23 41 0.51
5 51.14 51.65 51.40 16 0.2 57 0.71
6 51.65 52.16 51.91 20 0.25 77 0.96
7 52.16 52.67 52.42 2 0.03 79 0.99
8 52.67 53.18 52.93 1 0.01 80 1.00
Total 80 1.00
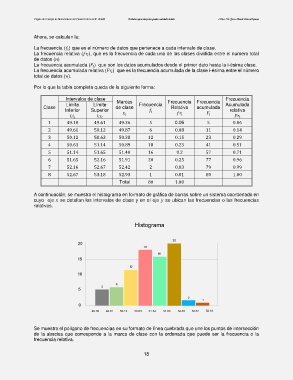
A continuación, se muestra el histograma en formato de gráfica de barras sobre un sistema coordenado en
cuyo eje se detallan los intervalos de clase y en el eje se ubican las frecuencias o las frecuencias
relativas.
Se muestra el polígono de frecuencias en su formato de línea quebrada que une los puntos de intersección
de la abscisa que corresponde a la marca de clase con la ordenada que puede ser la frecuencia o la
frecuencia relativa.
18