Page 4 - m5-unidad06-vectores
P. 4
Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Vectores Autor: Dr. José Manuel Becerra Espinosa
DETERMINACIÓN DE LAS COMPONENTES RECTANGULARES DE UN VECTOR EN EL PLANO
Las componentes rectangulares o cartesianas dan origen a dos vectores ficticios, que se conocen como
vectores componentes y , tal que sumados tengan como resultado el vector ⃗.
Los vectores componentes son:
⃗ = ⃗⃗⃗⃗⃗ + ⃗⃗⃗⃗⃗
Las componentes rectangulares del vector ⃗ en un plano, se pueden determinar usando las relaciones
trigonométricas de coseno y seno, obteniéndose las siguientes expresiones:
= |⃗| (Componente de ⃗ en el eje )
= |⃗| (Componente de ⃗ en el eje )
Por lo tanto el vector ⃗ queda expresado mediante sus componentes rectangulares de la siguiente forma:
⃗ = (|⃗| , |⃗| )
Ejemplo.
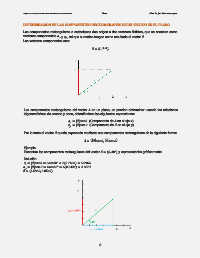
Encontrar las componentes rectangulares del vector ⃗ = (6, 40°) y representarlas gráficamente.
Solución.
= |⃗| = 640° = 6(0.7660) = 4.5962
= |⃗| = 640° = 6(0.6427) = 3.8567
⃗ = (4.5962, 3.8567)
3