Page 8 - m5-unidad06-vectores
P. 8
Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Vectores Autor: Dr. José Manuel Becerra Espinosa
Las coordenadas del punto de la figura son (, , ). La distancia denotada para se llama abscisa, se
llama ordenada y se llama cota. Los planos coordenados dividen al espacio en ocho regiones llamadas
octantes.
Los signos de las coordenadas se ilustran en la siguiente figura:
Un vector puede definirse en el espacio, conformado por tres líneas perpendiculares denominadas ejes.
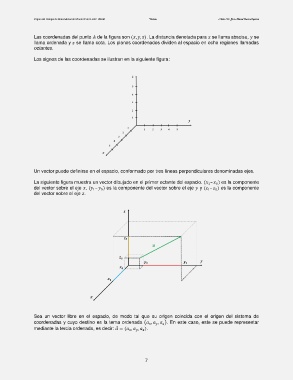
La siguiente figura muestra un vector dibujado en el primer octante del espacio. ( – ) es la componente
0
1
del vector sobre el eje , ( – ) es la componente del vector sobre el eje y ( – ) es la componente
1
0
0
1
del vector sobre el eje .
Sea un vector libre en el espacio, de modo tal que su origen coincida con el origen del sistema de
coordenadas y cuyo destino es la terna ordenada ( , , ). En este caso, este se puede representar
mediante la tercia ordenada, es decir: ⃗ = ( , , ).
7