Page 18 - m4-unidad05

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Inecuaciones para modelar restricciones Autor: Dr. José Manuel Becerra Espinosa

probando con dos números ubicados en esos intervalos para saber si cumplen la desigualdad 4x 2  4 x 1 0 :
 1  2
para x 0 del intervalo   ,  se tiene:   04  4   10   0  0  1 0
 2 
 1  2
para x 1 del intervalo  ,   se tiene:   14  4   11   4 4 1 1 0
 2 
Ninguno de los valores que cumplen la desigualdad, por lo que no tiene solución.

Nótese como la desigualdad 4x 2  4 x 1 0 se puede expresar como:
  x 2 2   12 x  0
2
Factorizando:
2
2 x  1  0
Puesto que el cuadrado de cualquier número real siempre es mayor o igual a cero, entonces se comprueba
que esta inecuación no tiene solución.

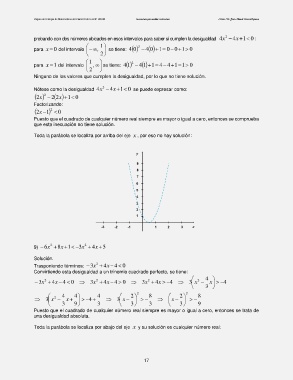
Toda la parábola se localiza por arriba del eje x , por eso no hay solución:

9) 6 x 2  8 x 1  3x 2  4 x 5

Solución.
Trasponiendo términos: 3 x 2  4 x 4  0
Convirtiendo esta desigualdad a un trinomio cuadrado perfecto, se tiene:
 4 
 3x 2  4 x 4  0  3x 2  4 x 4  0  3x 2  4 x  4  3 x 2   x   4
 3 
 4 4  4  2  2 8  2  2 8
 3 x 2  x     4   3 x      x   
 3 9  3  3  3  3  9
Puesto que el cuadrado de cualquier número real siempre es mayor o igual a cero, entonces se trata de
una desigualdad absoluta.

Toda la parábola se localiza por abajo del eje x y su solución es cualquier número real:

17