Page 34 - m5-unidad01

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Pensamiento geométrico para visualizar y argumentar Autor: Dr. José Manuel Becerra Espinosa

Lo que se pide es el cateto vertical, por lo que:

2
2
2
2
2
2
2
= +  = −  = 200 − 160 = 40,000 − 25,600 = 14,400
2
2
 = √14,400 = 120 .

4.3. RAZONES TRIGONOMÉTRICAS DIRECTAS E INVERSAS

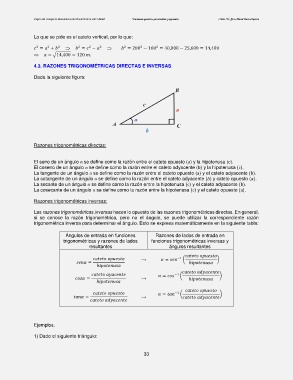
Dada la siguiente figura:

Razones trigonométricas directas:

El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).
El coseno de un ángulo α se define como la razón entre el cateto adyacente (b) y la hipotenusa (c).
La tangente de un ángulo α se define como la razón entre el cateto opuesto (a) y el cateto adyacente (b).
La cotangente de un ángulo α se define como la razón entre el cateto adyacente () y cateto opuesto ().
La secante de un ángulo α se define como la razón entre la hipotenusa (c) y el cateto adyacente (b).
La cosecante de un ángulo α se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).

Razones trigonométricas inversas:

Las razones trigonométricas inversas hacen lo opuesto de las razones trigonométricas directas. En general,
si se conoce la razón trigonométrica, pero no el ángulo, se puede utilizar la correspondiente razón
trigonométrica inversa para determinar el ángulo. Esto se expresa matemáticamente en la siguiente tabla:

Ángulos de entrada en funciones Razones de lados de entrada en
trigonométricas y razones de lados funciones trigonométricas inversas y
resultantes ángulos resultantes

→ = −1 ( )
= ℎ
ℎ

= −1 ( )
= → ℎ
ℎ

= −1 ( )
= →

Ejemplos.

1) Dado el siguiente triángulo:

33