Page 31 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

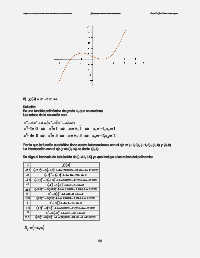
2) f ( ) = xx 4 − 5x 2 + 4
2

Solución.
Es una función polinómica de grado 4, que es continua.
Las raíces de la ecuación son:

x 4 − 5x 2 + 4 = (x 2 − 1 )(x 2 − 4 )= 0
x 2 − 1= 0  x 2 = 1  x =  1  x = , 1 − x = 1
1 2
x 2 − 4 = 0  x 2 = 4  x =  4  x = , 2 − x = 2
3 4

Por lo que la función cuadrática tiene cuatro intersecciones con el eje : (−2, 0), (−1, 0), (1, 0) y (2, 0).
La intersección con el eje es (0, ) es decir: (0, 4)
0

Se elige el intervalo de tabulación de [−2.5, 2.5] ya que incluye a las raíces del polinomio:

x f 2 ( ) x
-2.5 ( 2− ) 5 . 4 − 5 ( 2− ) 5 . 2 + 4 = 39 . 0625− 31 . 25 + 4 = 11 . 8125
-2 ( ) 2 −− 4 5 ( ) 2 +− 2 4 = 16 − 20 + 4 = 0
-1.5 ( 1− ) 5 . 4 − 5 ( 1− ) 5 . 2 + 4 = . 5 0625− 11 . 25 + 4 −= . 2 1875
-1 ( ) 1 −− 4 5 ( ) 1 +− 2 4 = 1− 5 + 4 = 0
-0.5 (−0.5) − 5(−0.5) + 4 = 0.0625 − 1.25 + 4 = 2.8125
2
4
2
4
0 0 − 5 ( ) 0 + 4 = 0 − 0 + 4 = 4
0.5 (0.5) − 5(0.5) + 4 = 0.0625 − 1.25 + 4 = 2.8125
2
4
2
1 1 − 5 ( ) 1 + 4 = 1− 5 + 4 = 0
4
1.5 ( ) 5.1 4 − 5 ( ) 5.1 2 + 4 = . 5 0625− 11 . 25 + 4 −= . 2 1875
2 2 − 5 ( ) 2 +− 2 4 = 16 − 20 + 4 = 0
4
2.5 ( ) 5.2 4 − 5 ( ) 5.2 2 + 4 = 39 . 0625− 31 . 25 + 4 = 11 . 8125

D f = ( − , ) 

30