Page 5 - m5-unidad12-hiperbola

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Hipérbola Autor: Dr. José Manuel Becerra Espinosa

3. LONGITUD DE LOS LADOS RECTOS DE UNA HIPÉRBOLA HORIZONTAL

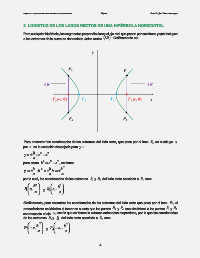
Para cualquier hipérbola, los segmentos perpendiculares al eje real que pasan por sus focos y que incluyen
LR
a los extremos de la curva se denominan lados rectos   . Gráficamente es:

Para encontrar las coordenadas de los extremos del lado recto, que pasa por el foco F , se sustituye x
1
por c en la ecuación despejada para y :
b
2
2
y   c  a
a
2
2
2
pero como b  c  a , se tiene:
b b b 2
2
y   b   b  
a a a
por lo cual, las coordenadas de los extremos P y P del lado recto asociado a F son:
2
1
1
 b 2   2 
P 1  c,  y P  c, b 


 a  2   a  

Similarmente, para encontrar las coordenadas de los extremos del lado recto que pasa por el foco F , el
2
procedimiento es idéntico al tomar en cuenta que los puntos P y P son simétricos a los puntos P y P
3
2
1
4
con respecto al eje x , con lo que se tienen la mismas ordenadas respectivas, por lo que las coordenadas
de los extremos P y P del lado recto asociado a F son:
3
4
2
 b 2   b 2 
P 3   c,  y P 4   c,  


 a    a  
4