Page 12 - m4-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Expresiones algebraicas para describir y generalizar Autor: Dr. José Manuel Becerra Espinosa

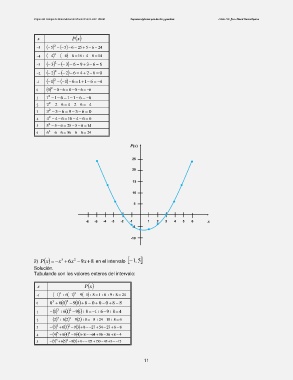
x P   x

5    5  2   65   25  5  6  24
4    4 2    64   16  4  6  14
3      633  2    9  3  6  6
2      622  2    4  2  6  0
1      611  2    1 1 6   4
2
0   0  0  6  0  0  6   6
2
1 1  1 6  1 1 6   6
2
2 2  2  6  4  2  6   4
2
3 3  3 6  9  3 6  0
2
4 4  4  6  16  4  6  6
5 5  5  6  25  5  6  14
2
6 6  6  6  36  6  6  24
2

2)    xxP 3  6x 2  9 x 8 en el intervalo  1,  5
Solución.
Tabulando con los valores enteros del intervalo:

x P   x
1     1  3 6   1  2 9   81   1 6  9  8  24
0 0  6   0 2  9   80   0  0  0  8  8
3
3
2
1    1  6   1  9   81    1 6 9 8  4
3
2
2    2  6   2  9   82    8 24  18  8  6
2
3    3  6   3  9   83    27  54  27  8  8
3
2
4    4  6   4  9   84    64  96  36  8  4
3
5    5  6   5  9   85    125  150  45  8   12
3
2
11