Page 14 - m4-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Expresiones algebraicas para describir y generalizar Autor: Dr. José Manuel Becerra Espinosa

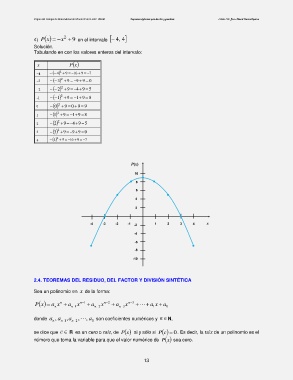
4)    xxP 2  9 en el intervalo  4,  4

Solución.
Tabulando en con los valores enteros del intervalo:

x P   x
4     4 2  9   16  9   7
3     3  2 9   9  9  0
2     2  2 9  4 9  5

1     1  2 9  1 9  8
2
0    0  9  0 9  9
2
1    1  9  1 9  8
2
2    2  9  4 9  5
2
3    3  9  9 9  0
2
4    4  9   16  9   7

2.4. TEOREMAS DEL RESIDUO, DEL FACTOR Y DIVISIÓN SINTÉTICA

Sea un polinomio en x de la forma:

n
P   ax  n x  a n 1 x n 1  a n 2 x n 2  a n 3 x n 3      a 1 x  a
0

donde a n , a n 1 ,a n 2 , , a son coeficientes numéricos y n N,
0

se dice que c R es un cero o raíz, de   xP si y sólo si   0cP . Es decir, la raíz de un polinomio es el
número que toma la variable para que el valor numérico de   xP sea cero.

13