Page 32 - m4-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Ecuaciones de primer y segundo grado para modelar condiciones específicas de una función Autor: Dr. José Manuel Becerra Espinosa

2
La ecuación y  ax  bx  c puede evaluarse para todo x R y por ello se unen los puntos obtenidos
para obtener sus gráficas.

Para fines prácticos, tabulando valores diferentes de x se pueden obtener los valores de y , generando puntos
de coordenadas  ,x  y que se localizan en el plano coordenado y que al unirse conforman la parábola.

Si las coordenadas de los puntos son grandes puede ser necesario modificar la escala en los ejes x y y ,
lo que provoca que las gráficas se deformen. Esto significa que su aspecto es diferente al que realmente
tienen.

Ejemplos.
Graficar las siguientes ecuaciones de segundo grado:

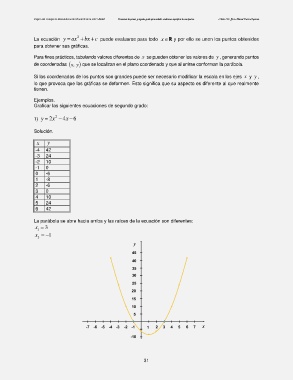
1) y 2x 2  4 x 6

Solución.

x y
-4 42
-3 24
-2 10
-1 0
0 -6
1 -8
2 -6
3 0
4 10
5 24
6 42

La parábola se abre hacia arriba y las raíces de la ecuación son diferentes:
x 1  3
x 2   1

31