Page 19 - m4-unidad04

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Sistemas de ecuaciones para modelar condiciones simultáneas Autor: Dr. José Manuel Becerra Espinosa

la recta pasa por los puntos  00 ., 6428  y  51 ,.  0
Para la segunda ecuación:
 3
Si x  0  2y   3  y    1. 5
2
 3
Si y 0  3 x  3  x    1
3
la recta pasa por los puntos 0, 1.  5 y  1,  0

graficando se obtiene que la solución es el punto de intersección  ,x  y , es decir  2, 1.  5
6   2 14    1251.  21  9 
comprobación: 
3      2 2 1. 5 6 3  3 

3x  3y  6 
3) 
5x 10y 10 

Solución
Para la primera ecuación:
6
Si x 0  3 y 6  y   2
3
6
Si y 0  3 x 6  x   2
3
la recta pasa por los puntos  20,  y  02, 
Para la segunda ecuación:
10
Si x 0   10 y 10  y    1
 10
10
Si y 0  5 x 10  x   2
5
la recta pasa por los puntos 0 ,  1 y  02, 

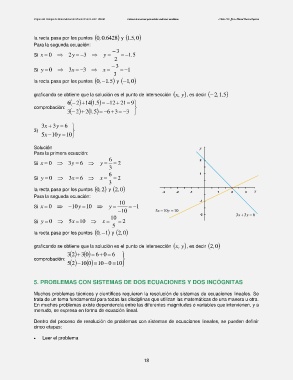
graficando se obtiene que la solución es el punto de intersección  ,x  y , es decir  02, 
3     032 6  0  6 
comprobación: 
5  102  100 0 10 

5. PROBLEMAS CON SISTEMAS DE DOS ECUACIONES Y DOS INCÓGNITAS

Muchos problemas técnicos y científicos requieren la resolución de sistemas de ecuaciones lineales. Se
trata de un tema fundamental para todas las disciplinas que utilizan las matemáticas de una manera u otra.
En muchos problemas existe dependencia entre las diferentes magnitudes o variables que intervienen, y a
menudo, se expresa en forma de ecuación lineal.

Dentro del proceso de resolución de problemas con sistemas de ecuaciones lineales, se pueden definir
cinco etapas:

 Leer el problema

18