Page 9 - m4-unidad04
P. 9
Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Sistemas de ecuaciones para modelar condiciones simultáneas Autor: Dr. José Manuel Becerra Espinosa
5
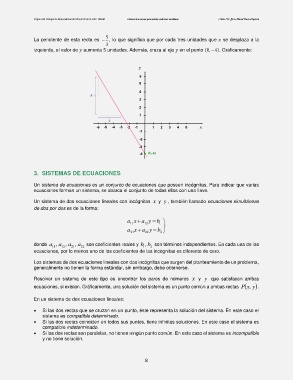
La pendiente de esta recta es , lo que significa que por cada tres unidades que se desplaza a la
3
izquierda, el valor de aumenta 5 unidades. Además, cruza al eje en el punto (0, −4). Gráficamente:
3. SISTEMAS DE ECUACIONES
Un sistema de ecuaciones es un conjunto de ecuaciones que poseen incógnitas. Para indicar que varias
ecuaciones forman un sistema, se abarca el conjunto de todas ellas con una llave.
Un sistema de dos ecuaciones lineales con incógnitas x y y , también llamado ecuaciones simultáneas
de dos por dos es de la forma:
a 11 x a 12 y b 1
a 21 x a 22 y b 2
donde a a , a , a , son coeficientes reales y ,b b son términos independientes. En cada una de las
11 12 21 22 1 2
ecuaciones, por lo menos uno de los coeficientes de las incógnitas es diferente de cero.
Los sistemas de dos ecuaciones lineales con dos incógnitas que surgen del planteamiento de un problema,
generalmente no tienen la forma estándar, sin embargo, debe obtenerse.
Resolver un sistema de este tipo es encontrar los pares de números x y y que satisfacen ambas
ecuaciones, si existen. Gráficamente, una solución del sistema es un punto común a ambas rectas y,xP .
En un sistema de dos ecuaciones lineales:
Si las dos rectas que se cruzan en un punto, éste representa la solución del sistema. En este caso el
sistema es compatible determinado.
Si las dos rectas coinciden en todos sus puntos, tiene infinitas soluciones. En este caso el sistema es
compatible indeterminado.
Si las dos rectas son paralelas, no tienen ningún punto común. En este caso el sistema es incompatible
y no tiene solución.
8