Page 15 - m5-unidad01

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Pensamiento geométrico para visualizar y argumentar Autor: Dr. José Manuel Becerra Espinosa

 = ≈ 1.618

A lo largo del tiempo, los artistas, en la búsqueda de composiciones perfectas, han dado con esta
proporción basada en la sección áurea, muy extendida en la naturaleza, que permite dividir el espacio en
partes proporcionales y lograr un efecto estético agradable.

Geométricamente, la sección áurea de un segmento se puede obtener mediante el siguiente
procedimiento:

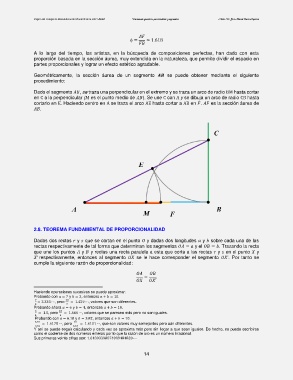
Dado el segmento , se traza una perpendicular en el extremo y se traza un arco de radio BM hasta cortar
en C a la perpendicular ( es el punto medio de ). Se une C con A y se dibuja un arco de radio CB hasta
cortarlo en E. Haciendo centro en A se traza el arco AE hasta cortar a AB en . es la sección áurea de
.

2.8. TEOREMA FUNDAMENTAL DE PROPORCIONALIDAD

Dadas dos rectas y que se cortan en el punto y dadas dos longitudes y sobre cada una de las
rectas respectivamente de tal forma que determinan los segmentos = y el = . Trazando la recta
que une los puntos y y rectas una recta paralela a esta que corta a las rectas y en el punto y
’ respectivamente, entonces al segmento se le hace corresponder el segmento ’. Por tanto se
cumple la siguiente razón de proporcionalidad:

=
′

Haciendo operaciones sucesivas se puede aproximar:
Probando con = 7 y = 3, entonces + = 10.
10
7
= 2.333⋯, pero = 1.429 ⋯, valores que son diferentes.
3 7
Probando ahora = 6 y = 4, entonces + = 10.
10
6
= 1.5, pero = 1.666⋯, valores que se parecen más pero no son iguales.
4 6
Probando con = 6.18 y = 3.82, entonces + = 10.
6.18 = 1.6178⋯, pero 10 = 1.6181⋯, que son valores muy semejantes pero aún diferentes.
3.82 6.18
Y así se puede seguir calculando y cada vez se aproxima más pero sin llegar a que sean iguales. De hecho, no puede escribirse
como el cociente de dos números enteros por lo que la razón de oro es un número irracional.
Sus primeras veinte cifras son: 1.61803398874989484820 ⋯

14