Page 11 - m5-unidad05-polares

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Coordenadas polares Autor: Dr. José Manuel Becerra Espinosa

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

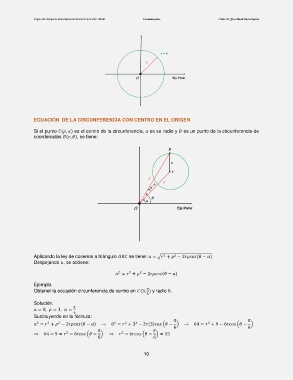
Si el punto (, ) es el centro de la circunferencia, es su radio y es un punto de la circunferencia de
coordenadas (, ), se tiene:

2
2
Aplicando la ley de cosenos a triángulo se tiene: = √ + − 2( − )
Despejando , se obtiene:

2
2
2
= + − 2( − )

Ejemplo.

Obtener la ecuación circunferencia de centro en (3, ) y radio 8.
6

Solución.

= 8, = 3, =
6
Sustituyendo en la fórmula:

2
2
2
2
2
= + − 2( − )  8 = + 3 − 2(3) ( − )  64 = + 9 − 6 ( − )
2
2
6 6

 64 − 9 = − 6 ( − )  − 6 ( − ) = 55
2
2
6 6

10