Page 9 - m5-unidad05-polares

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Coordenadas polares Autor: Dr. José Manuel Becerra Espinosa

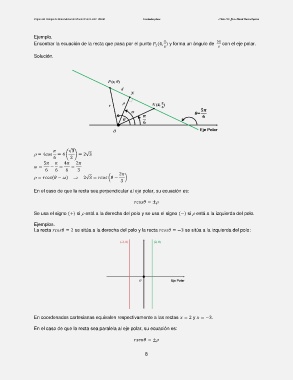
Ejemplo.
5

Encontrar la ecuación de la recta que pasa por el punto (4, ) y forma un ángulo de con el eje polar.
1
6 6

Solución.

√3
 = 4 = 4 ( ) = 2√3
6 2
5 4 2
= − = =
6 6 6 3
2
 = ( − )  2√3 = ( − )
3

En el caso de que la recta sea perpendicular al eje polar, su ecuación es:

= ±

Se usa el signo (+) si  está a la derecha del polo y se usa el signo (−) si  está a la izquierda del polo.

Ejemplos.
La recta = 2 se sitúa a la derecha del polo y la recta = −3 se sitúa a la izquierda del polo:

En coordenadas cartesianas equivalen respectivamente a las rectas = 2 y = −3.

En el caso de que la recta sea paralela al eje polar, su ecuación es:

= ±

8