Page 12 - m4-unidad05

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Inecuaciones para modelar restricciones Autor: Dr. José Manuel Becerra Espinosa

los intervalos solución pueden ser ( − , − ) 3 , ( 3,− ) 3 y ( ,3 )
probando con tres números ubicados en esos intervalos para saber si cumplen la desigualdad x 2 − 9  0 :
para =x − 4 del intervalo ( − , − ) 3 se tiene: ( ) 4 −− 2 9 = 16 − 9 = 7  0

2
para =x 0 del intervalo ( 3,− ) 3 se tiene: 0 − 9 = 0 − 9 = − 9  0
2
para =x 4 del intervalo ( ,3 ) se tiene: ( ) 4 − 9 = 16− 9 = 7  0
Los valores que cumplen la desigualdad son el primero y el tercero, por lo que la solución es:
( − , −3 ) ( ,3 ).

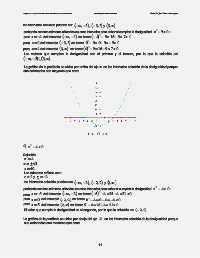
La gráfica de la parábola se ubica por arriba del eje x en los intervalos solución de la desigualdad porque
sus ordenadas son mayores que cero:

2) x 2 − 4  0

Solución.
x 2 = 4
= ±√4
x =  2
Los números críticos son:
r 1 = 2 y r 2 = − 2
los intervalos solución pueden ser ( − , − ) 2 , ( 2,− ) 2 y ( ,2 )
probando con tres números ubicados en esos intervalos para saber si cumplen la desigualdad x 2 − 4  0:
para =x − 5 del intervalo ( − , − ) 2 se tiene: ( ) 5 −− 2 4 = 25− 4 = 21 0
para =x 0 del intervalo ( 2,− ) 2 se tiene: 0 − 4 = 0 − 4 = − 4  0
2

para =x 5 del intervalo ( ,2 ) se tiene: 5 − 4 = 25− 4 = 21 0
2
El valor que cumple la desigualdad es el segundo, por lo que la solución es: ( 2,− ) 2 .

La gráfica de la parábola se ubica por abajo del eje x en los intervalos solución de la desigualdad porque
sus ordenadas son menores que cero:

11