Page 27 - m5-unidad02

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Álgebra para analizar los objetos geométricos Autor: Dr. José Manuel Becerra Espinosa

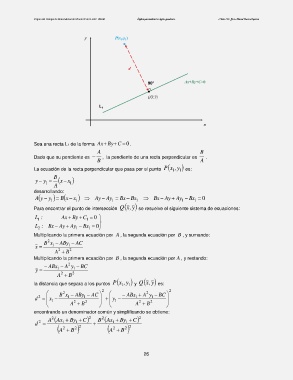
Sea una recta L1 de la forma Ax  By C  0 .

A B
Dado que su pendiente es  , la pendiente de una recta perpendicular es .
B A
La ecuación de la recta perpendicular que pasa por el punto  ,xP 1 y 1  es:
B

y  y  x  x 1
1
A
desarrollando:
A   yy 1  B   xx 1   Ay  Ay 1  Bx  Bx 1  Bx  Ay  Ay 1  Bx 1  0
Para encontrar el punto de intersección   y,xQ se resuelve el siguiente sistema de ecuaciones:

L 1 : Ax  By  C 1  0 
L 2 : Bx  Ay  Ay 1  Bx 1  0 

Multiplicando la primera ecuación por A , la segunda ecuación por B , y sumando:
B 2 x  ABy  AC
x  1 1
2
A  B 2
Multiplicando la primera ecuación por B , la segunda ecuación por A , y restando:
 ABx  A 2 y  BC
y  1 1
2
A  B 2
la distancia que separa a los puntos  ,xP 1 y 1  y   y,xQ es:

 B 2 x  ABy  AC  2   ABx  A 2 y  BC  2


d 2  x 1  1 1    y 1  1 1 



 A 2  B 2   A 2  B 2 
encontrando un denominador común y simplificando se obtiene:
2
1
1
1
d  A 2 Ax  By  C  2  B 2 Ax  By  C  2
1
2
2
A  B 2  2 A  B 2  2
26