Page 12 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

FUNCIONES CONTINUAS

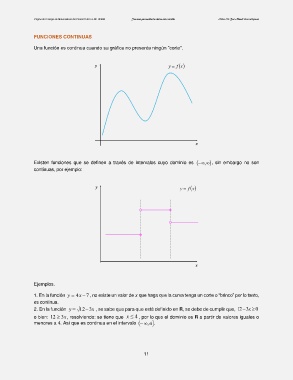
Una función es continua cuando su gráfica no presenta ningún “corte”.

Existen funciones que se definen a través de intervalos cuyo dominio es   ,  , sin embargo no son
continuas, por ejemplo:

Ejemplos.

1. En la función y  4 x 7 , no existe un valor de que haga que la curva tenga un corte o “brinco” por lo tanto,
es continua.
2. En la función y  12 3 x , se sabe que para que esté definido en R, se debe de cumplir que, 12  3 x 0
o bien: 12  3 x , resolviendo: se tiene que x 4 , por lo que el dominio es R a partir de valores iguales o
menores a 4. Así que es continua en el intervalo    4 , .

11