Page 13 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

FUNCIONES DISCONTINUAS

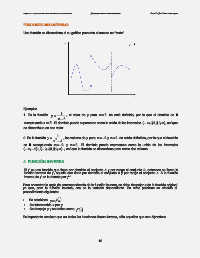
Una función es discontinua si su gráfica presenta al menos un “corte”.

Ejemplos.
1
1. En la función y  , el valor de para x  3 no está definido, por lo que el dominio es R
x  3
exceptuando x 3. El dominio puede expresarse como la unión de los intervalos   ,3   ,3 , así que
es discontinua en ese valor.

1
2. En la función y  , los valores de para x  2 y x 2 no están definidos, por lo que el dominio
x 2  4
es R exceptuando x   2 y x  2 . El dominio puede expresarse como la unión de los intervalos
   , 2   ,22   ,2  , así que la función es discontinua para estos dos valores.

4. FUNCIÓN INVERSA

Si es una función que tiene por dominio al conjunto y por rango al conjunto , entonces se llama la
función inversa de , aquella que tiene por dominio el conjunto y por rango al conjunto . A la función
inversa de se le denota por −1 .

Para encontrar la regla de correspondencia de la función inversa, se debe despejar de la función original
ya que, para la función inversa, esa es la variable dependiente. En otras palabras se efectúa el
procedimiento siguiente:

 Se establece y  f   x
 Se intercambia por .
 Se despeja y se define como f 1    x

Es importante recalcar que no todas las funciones tienen inversa, sólo aquellas que son biyectivas.

12