Page 19 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

donde y son constantes reales y es una variable real. La constante es la pendiente de la recta, y
es el punto de corte de la recta con el eje , que se conoce como ordenada al origen. Si se modifica
entonces se modifica la inclinación de la recta, y si se modifica , entonces la línea se desplazará hacia
arriba o hacia abajo.

Las funciones lineales son continuas y tanto su dominio como su rango son todos los números reales.

Una función lineal es creciente si tiene su pendiente positiva, es decreciente si tiene su pendiente negativa
y es constante si su pendiente es cero.

Ejemplos.
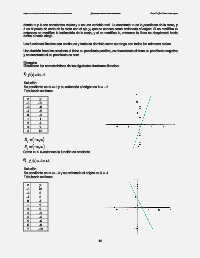
Establecer las características de las siguientes funciones lineales:

1) ( ) 3 −= xxf 2
1

Solución.
Su pendiente es = 3 y su ordenada al origen es = −2.
Tabulando se tiene:

-3 -11
-2 -8
-1 -5
0 -2
1 1
2 4
3 7
4 10

D = ( − , ) 
f
R f = ( − , ) 

Como > 0, entonces la función es creciente.

2) ( ) −=xf 2 +x 4
2

Solución.
Su pendiente es = −2 y su ordenada al origen es = 4.
Tabulando se tiene:

-3 10
-2 8
-1 6
0 4
1 2
2 0
3 -2
4 -4
5 -6
6 -8
7 -10

18