Page 23 - m5-unidad03

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Funciones para modelar la relación entre variables Autor: Dr. José Manuel Becerra Espinosa

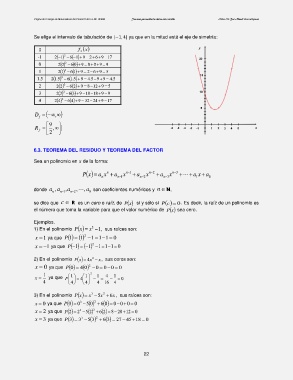
Se elige el intervalo de tabulación de [−1, 4] ya que en la mitad está el eje de simetría:

x
x f 3  
-1 2   1  2 6   91   2  6  9  17
2
0 2   0  6   90   0 0 9  9
1 2   1  6   91   2  6  9  5
2
1.5 2   5.1 2  6   95.1   5 . 4  9  9  5 . 4
2 2   2  6   92   8 12  9  5
2
2
3 2   3  6   93   18 18 9  9
2
4 2   4  6   94   32  24  9  17

D f    ,  

R f  9 ,   

 2


6.3. TEOREMA DEL RESIDUO Y TEOREMA DEL FACTOR

Sea un polinomio en de la forma:

n
P   ax  n x  a n 1 x n 1  a n 2 x n 2  a n 3 x n 3      a 1 x  a
0

donde a n , a n 1 ,a n 2 , , a son coeficientes numéricos y n N,
0

se dice que c R es un cero o raíz, de   xP si y sólo si   cP 0 . Es decir, la raíz de un polinomio es
el número que toma la variable para que el valor numérico de   xP sea cero.

Ejemplos.
1) En el polinomio   xxP 2  1, sus raíces son:
x  1 ya que     11 P 2  1 1 1 0
x   1 ya que     11 P  2  1 1 1 0

2
2) En el polinomio   xP  4 x  x, sus ceros son:
x  0 ya que   0 P 4   0 2  0  0  0  0
1  1   1  2 1 4 1
x  ya que P    4      0
4  4   4  4 16 4

3) En el polinomio   xxP  3  x 5 2  x 6 , sus raíces son:
2
x  0 ya que   00 P 3  5   0  6   00   0 0  0
2
x  2 ya que   22 P 3  5   2  6   82   20  12  0
2
x  3 ya que   33 P 3  5   3  6   3  27  45  18  0

22