Page 12 - m5-unidad06-vectores

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Vectores Autor: Dr. José Manuel Becerra Espinosa

|⃗| = √4 + 6 + 5 = √16 + 36 + 25 = √77
2
2
2

c) El vector unitario de ⃗ se obtiene con la siguiente expresión:

⃗ (4,6,5) 4 6 5
̂ = = = ( , , )
|| √77 √77 √77 √77

Cuando se trabaja en un sistema de coordenadas ortogonal (, , ) se definen los siguientes vectores
̂
unitarios: ̂(1,0,0), ̂(0,1,0), y (0,0,1), lo anterior significa que estos vectores se encuentra ubicados en cada
̂
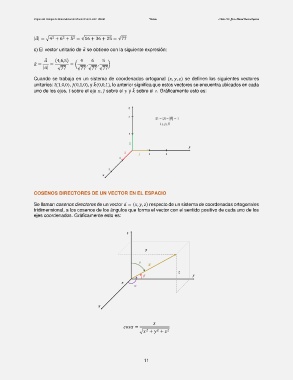
uno de los ejes, ̂ sobre el eje , ̂ sobre el y sobre el . Gráficamente esto es:

COSENOS DIRECTORES DE UN VECTOR EN EL ESPACIO

Se llaman cosenos directores de un vector ⃗ = (, , ) respecto de un sistema de coordenadas ortogonales
tridimensional, a los cosenos de los ángulos que forma el vector con el sentido positivo de cada uno de los
ejes coordenados. Gráficamente esto es:

=
2
2
√ + + 2

11