Page 9 - m5-unidad11-elipse

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Elipse Autor: Dr. José Manuel Becerra Espinosa

La longitud, medida en unidades lineales ( ) u , de cada lado recto viene dado por la diferencia de sus
abscisas. Por lo tanto:

2 b 2
LR =
a

Ejemplo.
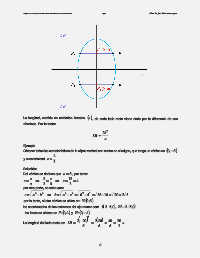
Obtener todas las características de la elipse vertical con centro en el origen, que tenga un vértice en (0 −, ) 6
2
y excentricidad =e .
3

Solución:
Del vértice se deduce que =a 6 , por tanto:
c 2 c 12
e =  =  c = = 4
a 3 6 3
por otra parte, se sabe que:
2
2
c = a 2 −b 2  b = a 2 −c 2 = 6 − 4 = 36− 16 = 20 = 2 5
por lo tanto, el otro vértice se ubica en: ( ) 60,V 1
las coordenadas de los extremos del eje menor son: (2B ) 0 , 5 , ( 2−B  ) 0 , 5
los focos se ubican en ( ) 40,F 1 y (0 −,F 2 ) 4

2 ( ) 2 2 ( ) 40 20
20
20
La longitud del lado recto es: LR = = = = . u
6 6 6 3

8