Page 13 - m5-unidad12-hiperbola

Página del Colegio de Matemáticas del Plantel 8 de la ENP-UNAM Hipérbola Autor: Dr. José Manuel Becerra Espinosa

' x  x  h y 'y  y  k

y sustituyendo en la ecuación anterior se tiene que:

  ky  2    hx  2  1
a 2 b 2

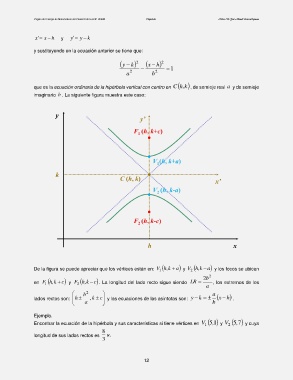
que es la ecuación ordinaria de la hipérbola vertical con centro en   k,hC , de semieje real a y de semieje
imaginario b . La siguiente figura muestra este caso:

De la figura se puede apreciar que los vértices están en:  k,hV 1   a y  k,hV 2   a y los focos se ubican

b 2 2
en  k,hF 1   c y F 2  k,h   c . La longitud del lado recto sigue siendo LR  , los extremos de los
a
 b 2  a
lados rectos son:  h k ,   c y las ecuaciones de las asíntotas son: y  k   x   h .


 a  b

Ejemplo.
Encontrar la ecuación de la hipérbola y sus características si tiene vértices en   15,V 1 y   75,V 2 y cuya
8
longitud de sus lados rectos es . u
3

12